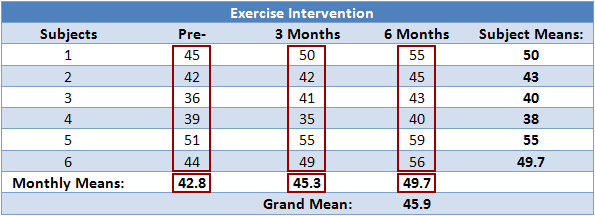
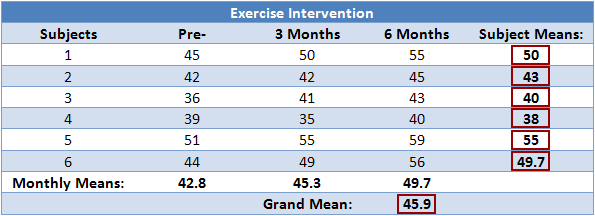
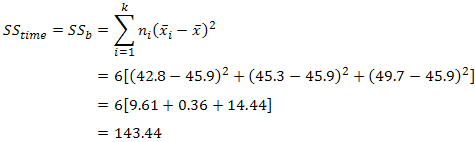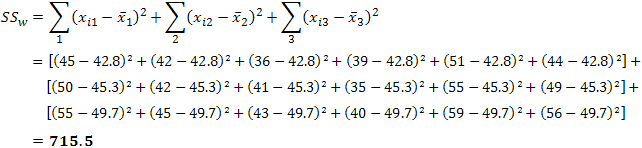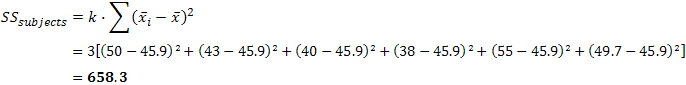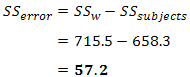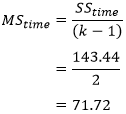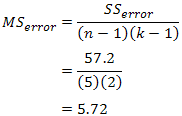| p.adjust {stats} | R Documentation |
Adjust P-values for Multiple Comparisons
Description
Given a set of p-values, returns p-values adjusted using one of several methods.Usage
p.adjust(p, method = p.adjust.methods, n = length(p))
p.adjust.methods
# c("holm", "hochberg", "hommel", "bonferroni", "BH", "BY",
# "fdr", "none")
Arguments
p |
numeric vector of p-values (possibly with NAs).
Any other R is coerced by as.numeric. |
method |
correction method. Can be abbreviated. |
n |
number of comparisons, must be at least length(p);
only set this (to non-default) when you know what you are doing! |
Details
The adjustment methods include the Bonferroni correction ("bonferroni") in which the p-values are multiplied by the
number of comparisons. Less conservative corrections are also
included by Holm (1979) ("holm"), Hochberg (1988)
("hochberg"), Hommel (1988) ("hommel"), Benjamini &
Hochberg (1995) ("BH" or its alias "fdr"), and Benjamini &
Yekutieli (2001) ("BY"), respectively.
A pass-through option ("none") is also included.
The set of methods are contained in the p.adjust.methods vector
for the benefit of methods that need to have the method as an option
and pass it on to p.adjust.
The first four methods are designed to give strong control of the family-wise error rate. There seems no reason to use the unmodified Bonferroni correction because it is dominated by Holm's method, which is also valid under arbitrary assumptions.
Hochberg's and Hommel's methods are valid when the hypothesis tests are independent or when they are non-negatively associated (Sarkar, 1998; Sarkar and Chang, 1997). Hommel's method is more powerful than Hochberg's, but the difference is usually small and the Hochberg p-values are faster to compute.
The
"BH" (aka "fdr") and "BY" method of
Benjamini, Hochberg, and Yekutieli control the false discovery rate,
the expected proportion of false discoveries amongst the rejected
hypotheses. The false discovery rate is a less stringent condition
than the family-wise error rate, so these methods are more powerful
than the others.
Note that you can set
n larger than length(p) which
means the unobserved p-values are assumed to be greater than all the
observed p for "bonferroni" and "holm" methods and equal
to 1 for the other methods.
Value
A numeric vector of corrected p-values (of the same length asp, with names copied from p).
References
Benjamini, Y., and Hochberg, Y. (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society Series B 57, 289–300.Benjamini, Y., and Yekutieli, D. (2001). The control of the false discovery rate in multiple testing under dependency. Annals of Statistics 29, 1165–1188.
Holm, S. (1979). A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics 6, 65–70.
Hommel, G. (1988). A stagewise rejective multiple test procedure based on a modified Bonferroni test. Biometrika 75, 383–386.
Hochberg, Y. (1988). A sharper Bonferroni procedure for multiple tests of significance. Biometrika 75, 800–803.
Shaffer, J. P. (1995). Multiple hypothesis testing. Annual Review of Psychology 46, 561–576. (An excellent review of the area.)
Sarkar, S. (1998). Some probability inequalities for ordered MTP2 random variables: a proof of Simes conjecture. Annals of Statistics 26, 494–504.
Sarkar, S., and Chang, C. K. (1997). Simes' method for multiple hypothesis testing with positively dependent test statistics. Journal of the American Statistical Association 92, 1601–1608.
Wright, S. P. (1992). Adjusted P-values for simultaneous inference. Biometrics 48, 1005–1013. (Explains the adjusted P-value approach.)
See Also
pairwise.* functions such as pairwise.t.test.
Examples
require(graphics)
set.seed(123)
x <- rnorm(50, mean = c(rep(0, 25), rep(3, 25)))
p <- 2*pnorm(sort(-abs(x)))
round(p, 3)
round(p.adjust(p), 3)
round(p.adjust(p, "BH"), 3)
## or all of them at once (dropping the "fdr" alias):
p.adjust.M <- p.adjust.methods[p.adjust.methods != "fdr"]
p.adj <- sapply(p.adjust.M, function(meth) p.adjust(p, meth))
p.adj.60 <- sapply(p.adjust.M, function(meth) p.adjust(p, meth, n = 60))
stopifnot(identical(p.adj[,"none"], p), p.adj <= p.adj.60)
round(p.adj, 3)
## or a bit nicer:
noquote(apply(p.adj, 2, format.pval, digits = 3))
## and a graphic:
matplot(p, p.adj, ylab="p.adjust(p, meth)", type = "l", asp = 1, lty = 1:6,
main = "P-value adjustments")
legend(0.7, 0.6, p.adjust.M, col = 1:6, lty = 1:6)
## Can work with NA's:
pN <- p; iN <- c(46, 47); pN[iN] <- NA
pN.a <- sapply(p.adjust.M, function(meth) p.adjust(pN, meth))
## The smallest 20 P-values all affected by the NA's :
round((pN.a / p.adj)[1:20, ] , 4)
[Package stats version 3.3.0 Index]